This content originally appeared on Level Up Coding – Medium and was authored by Sonika | @Walmart | FrontEnd Developer | 10 Years
Topic Covered:
Traversal Technique —
–Breadth-First Search (BFS)
-Depth-First Search (DFS)
Rotting Oranges (Breadth-First Search (BFS) approach)
Number of Islands (Depth-First Search (DFS) approach)
Max Area of Island Depth-First Search (DFS) approach)
Clone Graph (Depth-First Search (DFS) approach)
Walls And Gates ( Breadth-First Search (BFS) approach)
Surrounded Regions (DFS and BFS approach)
InProgress:
Pacific Atlantic Water Flow
Course Schedule(Detect Cycle approach)
Course Schedule II
Graph Valid Tree
Number of Connected Components In An Undirected Graph
Redundant Connection
Traversal Technique — Breadth-First Search (QUEUE- FIFO)
Approach,
- adjacencyList(Ask who are your neightbours): This represents our graph where each index corresponds to a node, and the array at each index contains the nodes to which it is directly connected.
- visited: An array initialized to false indicating whether each node has been visited.
- queue: An array used as a queue for BFS operations.
- bfs(startNode, adjacencyList): The BFS function takes a starting node (startNode) and the adjacency list of the graph. It initializes the queue with startNode, marks it as visited, and then continues to dequeue nodes from the front, visiting each node's neighbors in turn.
- While Loop: Continues until the queue is empty. It dequeues a node, marks it as visited, and enqueues its neighbors if they haven’t been visited yet.
Dry Run,

Starting BFS from node 0:
Dequeued node: 0
Current queue: []
queue: neighbors: [] (2) [1, 3]
Enqueued node: 1
Updated queue: [1]
Enqueued node: 3
Updated queue: (2) [1, 3]
Dequeued node: 1
Current queue: [3]
queue: neighbors: [3] (3) [0, 2, 4]
Enqueued node: 2
Updated queue: (2) [3, 2]
Enqueued node: 4
Updated queue: (3) [3, 2, 4]
Dequeued node: 3
Current queue: (2) [2, 4]
queue: neighbors: (2) [2, 4] [0]
Dequeued node: 2
Current queue: [4]
queue: neighbors: [4] (2) [1, 5]
Enqueued node: 5
Updated queue: (2) [4, 5]
Dequeued node: 4
Current queue: [5]
queue: neighbors: [5] (3) [1, 5, 7]
Enqueued node: 7
Updated queue: (2) [5, 7]
Dequeued node: 5
Current queue: [7]
queue: neighbors: [7] (3) [2, 4, 6]
Enqueued node: 6
Updated queue: (2) [7, 6]
Dequeued node: 7
Current queue: [6]
queue: neighbors: [6] [4]
Dequeued node: 6
Current queue: []
queue: neighbors: [] [5]
Traversal Technique — Depth-First Search (DFS) — Uses Recursion
Approach
- uses adjacency list
- uses recursion of dfs(…..)
DFS Function (dfs):
- dfs(node, adjacencyList, visited): This function performs the depth-first traversal starting from node. It marks the current node as visited, prints it (or performs any other desired operation), and recursively visits all its unvisited neighbors.
Initialization (startDFS):
- startDFS(startNode, adjacencyList): This function initializes the DFS traversal from startNode. It initializes the visited array to keep track of visited nodes and calls the dfs function to start the traversal.
Example Usage:
- startDFS(0, adjacencyList);: This initiates DFS starting from node 0 in the given adjacency list.
Starting DFS from node 0
Visited node: 0
Visited node: 1
Visited node: 2
Visited node: 5
Visited node: 6
Visited node: 4
Visited node: 7
Visited node: 3
Dry run,
// Example adjacency list representation of the graph
const adjacencyList = [
[1, 3], // Node 0 is connected to nodes 1 and 3
[0, 2, 4], // Node 1 is connected to nodes 0, 2, and 4
[1, 5], // Node 2 is connected to nodes 1 and 5
[0], // Node 3 is connected to node 0
[1, 5, 7], // Node 4 is connected to nodes 1, 5, and 7
[2, 4, 6], // Node 5 is connected to nodes 2, 4, and 6
[5], // Node 6 is connected to node 5
[4] // Node 7 is connected to node 4
];
// DFS function
function dfs(node, adjacencyList, visited) {
visited[node] = true;
console.log("Visited node:", node);
// Visit all neighbors of the current node recursively
const neighbors = adjacencyList[node];
for (let neighbor of neighbors) {
if (!visited[neighbor]) {
dfs(neighbor, adjacencyList, visited);
}
}
}
// Function to initialize DFS traversal
function startDFS(startNode, adjacencyList) {
const n = adjacencyList.length;
const visited = new Array(n).fill(false);
console.log("Starting DFS from node", startNode);
dfs(startNode, adjacencyList, visited);
}
// Example usage:
startDFS(0, adjacencyList);
Rotting Oranges
Which DFS or BFS ?
https://leetcode.com/problems/rotting-oranges/description/
You are given a 2-D matrix grid. Each cell can have one of three possible values:
- 0 representing an empty cell
- 1 representing a fresh fruit
- 2 representing a rotten fruit
Every second, if a fresh fruit is horizontally or vertically adjacent to a rotten fruit, then the fresh fruit also becomes rotten.
Return the minimum number of seconds that must elapse until there are zero fresh fruits remaining. If this state is impossible within the grid, return -1.
Example 1:
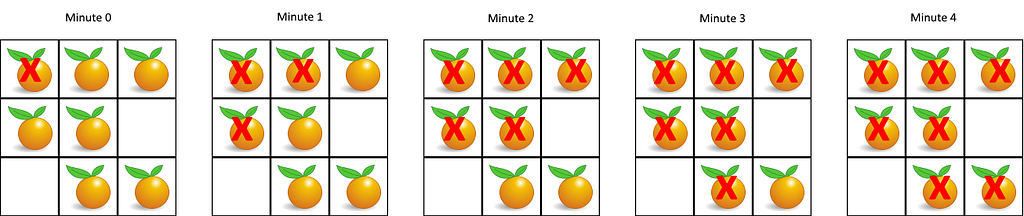
Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4
Example 2:
Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
Utilize a Breadth-First Search (BFS) approach — queue, examine its neighboring cells (up, down, left, right)
Approach,
Initialization:
- We’ll use a queue to perform BFS. Initially, we’ll enqueue all cells that contain rotten fruits (2) because these will be our starting points.
BFS Execution:
- We will dequeue each cell from the queue, examine its neighboring cells (up, down, left, right), and attempt to infect neighboring fresh fruits (1) to rotten (2).
- For each infected fresh fruit, we mark it as rotten and enqueue it to continue the infection process in subsequent seconds.
Tracking Time:
- We’ll maintain a time variable to count the number of seconds (iterations of BFS) required for the infection to spread.
Completion Check:
- If we successfully infect all fresh fruits, the BFS will terminate naturally, and we return the time.
- If there are fresh fruits left after BFS completes (queue is empty), it means some fresh fruits are unreachable from any rotten fruit, and we return -1 indicating it's impossible to infect all fresh fruits.
Complexity:
- Time Complexity: O(m×n), where m and n are the dimensions of the grid. This is because in the worst case, we might process every cell in the grid during BFS.
- Space Complexity: O(m×n) due to the queue and potentially modifying the grid in place.
Implementation,

function orangesRotting(grid) {
const rows = grid.length;
const cols = grid[0].length;
// Directions for moving up, down, left, right
const directions = [[-1, 0], [1, 0], [0, -1], [0, 1]];
// Initialize queue for BFS and count fresh oranges
const queue = [];
let freshCount = 0;
// Enqueue all rotten oranges and count fresh oranges
for (let i = 0; i < rows; i++) {
for (let j = 0; j < cols; j++) {
if (grid[i][j] === 2) {
queue.push([i, j, 0]); // [row, col, time]
} else if (grid[i][j] === 1) {
freshCount++;
}
}
}
// BFS to infect fresh oranges
let time = 0;
while (queue.length > 0) {
const [row, col, currentTime] = queue.shift();
time = currentTime; // Update time to the current time
for (const [dx, dy] of directions) {
const newRow = row + dx;
const newCol = col + dy;
if (newRow >= 0 && newRow < rows && newCol >= 0 && newCol < cols) {
if (grid[newRow][newCol] === 1) { // Fresh orange found
grid[newRow][newCol] = 2; // Infect it
freshCount--;
queue.push([newRow, newCol, currentTime + 1]);
}
}
}
}
// If there are fresh oranges left, return -1
if (freshCount > 0) {
return -1;
}
return time; // Return the minimum time required
}
// Example usage:
const grid = [
[2,1,1],
[1,1,0],
[0,1,1]
];
console.log(orangesRotting(grid)); // Output: 4
Number of Islands-
Which DFS or BFS ?
https://leetcode.com/problems/number-of-islands/
Given an m x n 2D binary grid grid which represents a map of '1's (land) and '0's (water), return the number of islands.
An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example 1:
Input: grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
Output: 1
Example 2:
Input: grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
Output: 3
Utilize a Depth-First Search (BFS) approach — recursion, examine its neighboring cells (up, down, left, right)
Approach,
- Traverse each cell in the grid.
- When a ‘1’ is encountered, initiate a DFS to mark all connected ‘1’s as visited (by setting them to ‘0’).
- Increment the island count for each DFS initiation.
Implementation,
function numIslands(grid) {
if (grid === null || grid.length === 0) {
return 0;
}
let numberOfIslands = 0;
const dfs = function (grid, i, j) {
if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] === '0') {
return;
}
grid[i][j] = '0'; // Mark the cell as visited
// Visit all adjacent cells (up, down, left, right)
dfs(grid, i - 1, j); // up
dfs(grid, i + 1, j); // down
dfs(grid, i, j - 1); // left
dfs(grid, i, j + 1); // right
};
for (let i = 0; i < grid.length; i++) {
for (let j = 0; j < grid[0].length; j++) {
if (grid[i][j] === '1') {
numberOfIslands++;
dfs(grid, i, j); // Start DFS to mark all parts of this island
}
}
}
return numberOfIslands;
}
// Example usage:
const grid = [
["1", "1", "1", "1", "0"],
["1", "1", "0", "1", "0"],
["1", "1", "0", "0", "0"],
["0", "0", "0", "0", "0"]
];
console.log(numIslands(grid)); // Output: 1
Max Area of Island
Which DFS or BFS ?
https://leetcode.com/problems/max-area-of-island/description/
You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
The area of an island is the number of cells with a value 1 in the island.
Return the maximum area of an island in grid. If there is no island, return 0.
Example 1:

Input: grid = [
[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]
]
Output: 6
Explanation: The answer is not 11, because the island must be connected
4-directionally.
Example 2:
Input: grid = [[0,0,0,0,0,0,0,0]]
Output: 0
use Depth-First Search (DFS) to traverse each cell of the grid and calculate the area of each island encountered.
Approach,
- Grid Traversal: Traverse each cell in the grid.
- DFS for Area Calculation: When a ‘1’ (land) is encountered, initiate a DFS to mark all connected ‘1’s as visited and calculate the area of the island.
- Track Maximum Area: Keep track of the maximum area encountered during the traversal.
Implementation,
function maxAreaOfIsland(grid) {
if (grid === null || grid.length === 0) {
return 0;
}
let maxArea = 0;
const dfs = function (grid, i, j) {
if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] === 0) {
return 0;
}
grid[i][j] = 0; // Mark the cell as visited
let area = 1; // Current cell
// Visit all adjacent cells (up, down, left, right)
area += dfs(grid, i - 1, j); // up
area += dfs(grid, i + 1, j); // down
area += dfs(grid, i, j - 1); // left
area += dfs(grid, i, j + 1); // right
return area;
};
for (let i = 0; i < grid.length; i++) {
for (let j = 0; j < grid[0].length; j++) {
if (grid[i][j] === 1) {
const currentArea = dfs(grid, i, j);
maxArea = Math.max(maxArea, currentArea);
}
}
}
return maxArea;
}
// Example usage:
const grid = [
[0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0],
[0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0],
[0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0]
];
console.log(maxAreaOfIsland(grid)); // Output: 6
Clone Graph
https://leetcode.com/problems/clone-graph/description/
Given a reference of a node in a connected undirected graph.
Return a deep copy (clone) of the graph.
Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.
Example 1:

Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
Approach,
Recursive Depth-First Search (DFS) algorithm.
- Maintain map called visited to keep track of visited nodes and their corresponding clones.
- Traverse the graph recursively, creayed a clone of each node encountered and store it in the visited map.
- When visiting a node’s neighbour's, I recursively clone each neighbour and add it to the cloned node’s neighbours array.
Implementation,
function Node(val, neighbors) {
this.val = val === undefined ? 0 : val;
this.neighbors = neighbors === undefined ? [] : neighbors;
};
var cloneGraph = function(node) {
if (node == null) {
return null;
}
let visited = new Map();
function dfs(node) {
if (visited.has(node)) {
return visited.get(node);
}
let clone = new Node(node.val);
visited.set(node, clone);
for (let neighbor of node.neighbors) {
clone.neighbors.push(dfs(neighbor));
}
return clone;
}
return dfs(node);
};
Walls And Gates — Breadth-First Search (BFS)
https://neetcode.io/problems/islands-and-treasure
You are given a 𝑚×𝑛m×n 2D grid initialized with these three possible values:
- -1 – A water cell that can not be traversed.
- 0 – A treasure chest.
- INF – A land cell that can be traversed. We use the integer 2^31 – 1 = 2147483647 to represent INF.
Fill each land cell with the distance to its nearest treasure chest. If a land cell cannot reach a treasure chest than the value should remain INF.
Assume the grid can only be traversed up, down, left, or right.
Example 1:
Input: [
[2147483647,-1,0,2147483647],
[2147483647,2147483647,2147483647,-1],
[2147483647,-1,2147483647,-1],
[0,-1,2147483647,2147483647]
]
Output: [
[3,-1,0,1],
[2,2,1,-1],
[1,-1,2,-1],
[0,-1,3,4]
]
Approach,
Use the Breadth-First Search (BFS) algorithm. BFS is particularly well-suited for finding the shortest path in an unweighted grid, as it explores all possible paths level by level.
- First, we identify all gate locations as starting points since we need to find the minimum distance from these gates to each room.
- We put all these gate coordinates in a queue for BFS processing. Since BFS processes elements level-by-level, it’s perfect for measuring increasing distances from a starting point (in this case, the gates).
- We pop coordinates from the queue and explore its neighbors (rooms to the left, right, up, and down). If we find an empty room (with INF), it's apparent that this is the first time we reach this room (as the queue ensures the shortest paths are explored first), so we update the room's value to the current distance.
- Since gates serve as the origin, distances increase as we move away from them. Each level deeper in the search increases the distance by one.
- Neighbors that are walls or already visited with a smaller distance are skipped, as we are looking for the shortest path to a gate. We continue this process until there are no more rooms to explore.
Example Walkthrough
Let’s illustrate the solution approach using a simple 3×3 grid example where -1 represents a wall, 0 represents a gate, and INF (represented as 2147483647 for the purpose of example) represents an empty room that needs its distance filled to the nearest gate.
Consider the following grid:
1. INF -1 0
2. INF INF INF
3. INF -1 INF
Here’s how the Breadth-First Search (BFS) algorithm would update this grid:
Initialization:
- We identify the gate at grid[0][2] and add its coordinates to the queue.
BFS Implementation:
- Start with the gate in the queue: (0, 2).
Neighbor Checks:
- The gate at (0, 2) has three neighbors: (0, 1), (0, 3), and (1, 2).
- However, (0, 1) is a wall and (0, 3) is out of bounds, so we only consider (1, 2).
- Since (1, 2) is INF, we update it to the distance 1 (the current level), and add (1, 2) to the queue.
The grid now looks like this:
1. INF -1 0
2. INF INF 1
3. INF -1 INF
Distance Increment:
- Increment d to 2 for the next level of rooms.
Continue BFS:
- Now, (1, 2) is the only room in the queue. Its neighbors are (1, 1), (1, 3), (0, 2), and (2, 2).
- (1, 1) is updatable and becomes 2.
- (1, 3) is out of bounds.
- (0, 2) is a gate and already has the shortest distance.
- (2, 2) is updatable and becomes 2.
Add (1, 1) and (2, 2) to the queue.
The grid now looks like this:
1. INF -1 0
2 2 INF 1
3. INF -1 2
Distance Increment:
- Increment d to 3.
Next BFS level:
- For (1, 1), neighbors are (1, 0), (1, 2), (0, 1), and (2, 1).
- (1, 0) is updatable and becomes 3.
- (2, 1) is updatable and becomes 3.
For (2, 2), the only neighbor not already checked or out of bounds is (2, 1), but it’s already been updated this level.
Final updated grid:
1 INF -1 0
2 3 2 1
3 INF -1 2
Notice that the top left room remains INF, as it is inaccessible. All other rooms have been updated to show the shortest path to the nearest gate.
Implementation,
const directions = [
[1, 0], // down
[-1, 0], // up
[0, 1], // right
[0, -1] // left
];
function treasureDistances(grid) {
if (!grid || grid.length === 0 || grid[0].length === 0) {
return;
}
const m = grid.length;
const n = grid[0].length;
const queue = [];
// Initialize the queue with all the treasure chests (0's)
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (grid[i][j] === 0) {
queue.push([i, j]);
}
}
}
// Perform BFS from all treasure chests
while (queue.length > 0) {
const [x, y] = queue.shift();
for (const [dx, dy] of directions) {
const newX = x + dx;
const newY = y + dy;
if (newX >= 0 && newX < m && newY >= 0 && newY < n && grid[newX][newY] === 2147483647) {
grid[newX][newY] = grid[x][y] + 1; // Update distance
queue.push([newX, newY]); // Push the new cell to the queue
}
}
}
return grid;
}
// Example usage:
const grid = [
[2147483647, -1, 0, 2147483647],
[2147483647, 2147483647, 2147483647, -1],
[2147483647, -1, 2147483647, -1],
[0, -1, 2147483647, 2147483647]
];
console.log(treasureDistances(grid));
Surrounded Regions (DFS and BFS)
https://leetcode.com/problems/surrounded-regions/description/
You are given an m x n matrix board containing letters 'X' and 'O', capture regions that are surrounded:
- Connect: A cell is connected to adjacent cells horizontally or vertically.
- Region: To form a region connect every 'O' cell.
- Surround: The region is surrounded with 'X' cells if you can connect the region with 'X' cells and none of the region cells are on the edge of the board.
A surrounded region is captured by replacing all 'O's with 'X's in the input matrix board.

Input: board = [
["X","X","X","X"],
["X","O","O","X"],
["X","X","O","X"],
["X","O","X","X"]
]
Output: [
["X","X","X","X"],
["X","X","X","X"],
["X","X","X","X"],
["X","O","X","X"]
]
Use Depth-First Search (DFS) or Breadth-First Search (BFS).
The idea is to identify ‘O’s that are connected to the border and cannot be surrounded, then mark them.
Finally, flip the remaining ‘O’s to ‘X’s, as they represent surrounded regions.
Approach, (DFS)
- Mark Non-surrounded Regions: Traverse the border cells and mark all ‘O’s connected to the border with a temporary marker (e.g., ‘T’). This helps identify which ‘O’s are not surrounded.
- Flip the Remaining ‘O’s: Traverse the entire board and flip all remaining ‘O’s to ‘X’ and convert the temporary markers back to ‘O’.
This code is part of a strategy to mark all ‘O’ cells that are connected to the border of a grid. The dfs function (Depth-First Search) is used to explore and mark these cells.
Understand about these loops:
First Loop (for (let i = 0; i < m; i++)):
Purpose: To start a DFS from all ‘O’ cells on the leftmost and rightmost columns.
- dfs(i, 0): This starts a DFS from the cell in the i-th row and 0-th column (leftmost column).
- dfs(i, n – 1): This starts a DFS from the cell in the i-th row and (n – 1)-th column (rightmost column).
Second Loop (for (let j = 0; j < n; j++)):
- Purpose: To start a DFS from all ‘O’ cells on the topmost and bottommost rows.
- dfs(0, j): This starts a DFS from the cell in the 0-th row and j-th column (topmost row).
- dfs(m – 1, j): This starts a DFS from the cell in the (m – 1)-th row and j-th column (bottommost row).
Implementation
Purpose of These Loops: The primary goal of these loops is to identify all ‘O’ cells that are connected to the border and mark them. These cells (and the regions they are part of) should not be flipped to ‘X’ because they are not surrounded by ‘X’ on all sides.
Temporarily mark border-connected 'O's (e.g., with 'T'):
Example,
X X X X
X O O X
X X O X
T O X X <-- 'O' in the last row and first column is marked
function solve(board) {
// If the board is empty, return immediately
if (board.length === 0) {
return;
}
const m = board.length; // Number of rows
const n = board[0].length; // Number of columns
// Directions for moving up, down, left, right
const directions = [
[1, 0], // down
[-1, 0], // up
[0, 1], // right
[0, -1] // left
];
// Depth-First Search (DFS) function to mark connected 'O's starting from (x, y)
function dfs(x, y) {
// If out of bounds or not an 'O', return
if (x < 0 || x >= m || y < 0 || y >= n || board[x][y] !== 'O') {
return;
}
board[x][y] = 'T'; // Mark the cell as temporary ('T') to indicate it has been visited
// Recursively visit all connected 'O' cells
for (const [dx, dy] of directions) {
dfs(x + dx, y + dy);
}
}
// Start DFS from all 'O's on the border (left and right edges)
for (let i = 0; i < m; i++) {
dfs(i, 0); // Left edge
dfs(i, n - 1); // Right edge
}
// Start DFS from all 'O's on the border (top and bottom edges)
for (let j = 0; j < n; j++) {
dfs(0, j); // Top edge
dfs(m - 1, j); // Bottom edge
}
// Traverse the entire board to flip 'O' to 'X' and 'T' back to 'O'
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (board[i][j] === 'O') {
board[i][j] = 'X'; // Flip surrounded 'O' to 'X'
} else if (board[i][j] === 'T') {
board[i][j] = 'O'; // Convert temporary marker 'T' back to 'O'
}
}
}
}
// Example usage:
const board = [
['X', 'X', 'X', 'X'],
['X', 'O', 'O', 'X'],
['X', 'X', 'O', 'X'],
['X', 'O', 'X', 'X']
];
solve(board);
console.log(board);
// Output: [
// ['X', 'X', 'X', 'X'],
// ['X', 'X', 'X', 'X'],
// ['X', 'X', 'X', 'X'],
// ['X', 'O', 'X', 'X']
// ]
BFS,
function solve(board) {
// If the board is empty, return immediately
if (board.length === 0) {
return;
}
const m = board.length; // Number of rows
const n = board[0].length; // Number of columns
// Directions for moving up, down, left, right
const directions = [
[1, 0], // down
[-1, 0], // up
[0, 1], // right
[0, -1] // left
];
// Breadth-First Search (BFS) function to mark connected 'O's starting from (x, y)
function bfs(x, y) {
const queue = [[x, y]];
board[x][y] = 'T'; // Mark the cell as temporary ('T') to indicate it has been visited
while (queue.length > 0) {
const [cx, cy] = queue.shift();
for (const [dx, dy] of directions) {
const nx = cx + dx;
const ny = cy + dy;
// If within bounds and the cell is 'O', mark it and add to queue
if (nx >= 0 && nx < m && ny >= 0 && ny < n && board[nx][ny] === 'O') {
board[nx][ny] = 'T'; // Mark as temporary
queue.push([nx, ny]);
}
}
}
}
// Start BFS from all 'O's on the border (left and right edges)
for (let i = 0; i < m; i++) {
if (board[i][0] === 'O') bfs(i, 0); // Left edge
if (board[i][n - 1] === 'O') bfs(i, n - 1); // Right edge
}
// Start BFS from all 'O's on the border (top and bottom edges)
for (let j = 0; j < n; j++) {
if (board[0][j] === 'O') bfs(0, j); // Top edge
if (board[m - 1][j] === 'O') bfs(m - 1, j); // Bottom edge
}
// Traverse the entire board to flip 'O' to 'X' and 'T' back to 'O'
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (board[i][j] === 'O') {
board[i][j] = 'X'; // Flip surrounded 'O' to 'X'
} else if (board[i][j] === 'T') {
board[i][j] = 'O'; // Convert temporary marker 'T' back to 'O'
}
}
}
}
// Example usage:
const board = [
['X', 'X', 'X', 'X'],
['X', 'O', 'O', 'X'],
['X', 'X', 'O', 'X'],
['X', 'O', 'X', 'X']
];
solve(board);
console.log(board);
// Output: [
// ['X', 'X', 'X', 'X'],
// ['X', 'X', 'X', 'X'],
// ['X', 'X', 'X', 'X'],
// ['X', 'O', 'X', 'X']
// ]Pacific Atlantic Water Flow
https://leetcode.com/problems/pacific-atlantic-water-flow/description/
There is an m x n rectangular island that borders both the Pacific Ocean and Atlantic Ocean. The Pacific Ocean touches the island's left and top edges, and the Atlantic Ocean touches the island's right and bottom edges.
The island is partitioned into a grid of square cells. You are given an m x n integer matrix heights where heights[r][c] represents the height above sea level of the cell at coordinate (r, c).
The island receives a lot of rain, and the rain water can flow to neighboring cells directly north, south, east, and west if the neighboring cell’s height is less than or equal to the current cell’s height. Water can flow from any cell adjacent to an ocean into the ocean.
Return a 2D list of grid coordinates result where result[i] = [ri, ci] denotes that rain water can flow from cell (ri, ci) to both the Pacific and Atlantic oceans.
Example 1:
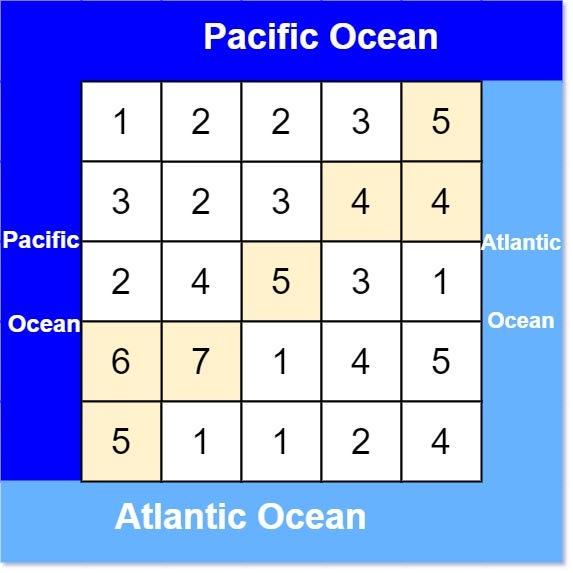
Input: heights = [
[1,2,2,3,5],
[3,2,3,4,4],
[2,4,5,3,1],
[6,7,1,4,5],
[5,1,1,2,4]
]
Output: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
Explanation: The following cells can flow to the
Pacific and Atlantic oceans, as shown below:
[0,4]: [0,4] -> Pacific Ocean
[0,4] -> Atlantic Ocean
[1,3]: [1,3] -> [0,3] -> Pacific Ocean
[1,3] -> [1,4] -> Atlantic Ocean
[1,4]: [1,4] -> [1,3] -> [0,3] -> Pacific Ocean
[1,4] -> Atlantic Ocean
[2,2]: [2,2] -> [1,2] -> [0,2] -> Pacific Ocean
[2,2] -> [2,3] -> [2,4] -> Atlantic Ocean
[3,0]: [3,0] -> Pacific Ocean
[3,0] -> [4,0] -> Atlantic Ocean
[3,1]: [3,1] -> [3,0] -> Pacific Ocean
[3,1] -> [4,1] -> Atlantic Ocean
[4,0]: [4,0] -> Pacific Ocean
[4,0] -> Atlantic Ocean
Note that there are other possible paths
for these cells to flow to the Pacific and Atlantic oceans.
Approach,
use Depth-First Search (DFS)
Initialize Sets: Use two sets to keep track of cells that can flow to the Pacific and Atlantic oceans.
- DFS Traversal: Perform DFS from the cells adjacent to the Pacific and Atlantic oceans.
- Mark Reachable Cells: During DFS, mark cells that are reachable from the ocean based on the height condition.
- Intersection: The result is the intersection of cells that can flow to both oceans.
In Progress……
Course Schedule [DETECT CYCLE]
https://leetcode.com/problems/course-schedule/description/
There are a total of numCourses courses you have to take, labeled from 0 to numCourses – 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course bi first if you want to take course ai.
- For example, the pair [0, 1], indicates that to take course 0 you have to first take course 1.
Return true if you can finish all courses. Otherwise, return false.
Example 1:
Input: numCourses = 2, prerequisites = [[1,0]]
Output: true
Explanation: There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.
Example 2:
Input: numCourses = 2, prerequisites = [[1,0],[0,1]]
Output: false
Explanation: There are a total of 2 courses to take.
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.

To solve this problem, you can use a graph-based approach to detect if there is a cycle in the course prerequisite graph. If there’s a cycle, it’s impossible to finish all courses; otherwise, it is possible.
Check — Topological Sort — Detect Cycle In Directed Graph
InProgress…
Number of Connected Components In An Undirected Graph
Thanks for reading
- Let’s Connect on Preplaced.com, Book Your Free Trial!
 Please clap for the story and follow me
Please clap for the story and follow me 
 View more content on Coding and System Design Interviews
View more content on Coding and System Design Interviews Follow me: LinkedIn!
Follow me: LinkedIn!
I know there would always be something to improve. Please feel free to share your thoughts
DSA | GRAPH was originally published in Level Up Coding on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content originally appeared on Level Up Coding – Medium and was authored by Sonika | @Walmart | FrontEnd Developer | 10 Years