This content originally appeared on DEV Community and was authored by Developer Harsh
As an AI enthusiast in, I’ve been closely following the recent developments in large language models. Today, I’m diving into a detailed comparison between two powerful contenders: Deep Seek V3 and Claude 3.7 Base.
Both models have been making waves in the AI community, but how do they actually perform across various coding tasks? Let’s decode the hype.
Deep Seek V3 Details
Deep Seek V3 is released recently as next addition to the deep seek family. Here are some key details worth noting:
 671B MoE parameters
671B MoE parameters 37B activated parameters
37B activated parameters Trained on 14.8T high-quality tokens
Trained on 14.8T high-quality tokens
 3x faster than V2! – 60 tokens / second
3x faster than V2! – 60 tokens / second Open Sources under MIT License
Open Sources under MIT License
To Learn More:
- Model: https://github.com/deepseek-ai/DeepSeek-V3
- Paper: https://github.com/deepseek-ai/DeepSeek-V3/blob/main/DeepSeek_V3.pdf
Having known the specifications, let’s now evaluate the model’s performance.
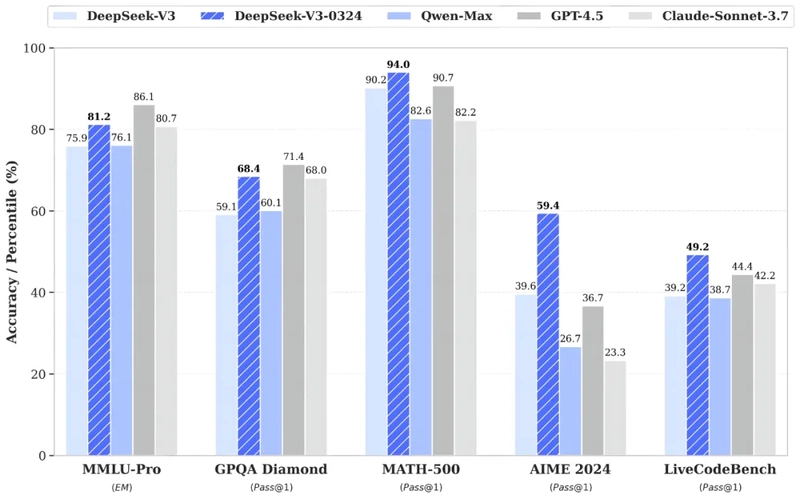
Evaluating Coding Performances
As we are going to compare the model against Claude 3.7 Base, which is beast in terms of coding, let’s compare deep seek V3 performance against same benchmarks for a level comparison.
For the evaluation test, I will be taking 4-5 examples from my set of curated ones and check the performance of both the models on the task given. Additionally, points will be given to winners. In case of tie 1 each contender receives 1 point.
We will compare the output based on code length, quality and response quality.
So, let’s start!
Test 1: 3js simulation
Prompt: Create a 3JS simulation of a metropolitan cityscape.
This test shows how good a model is at 3JS and their internal creativity. This is a zero-shot test, so all the simulation code was generated in one go. Here are the responses from the respective models.
Deepseek v3 0324:
The generated cityscape is clean, and the buildings, roads, and even traffic are defined. Though the movements weren’t working, the traffic toggle was working fine.
Claude 3.7 Sonnet:
The buildings and roads are less detailed than Deepseeks’s, but the movement worked; it was a first-person perspective simulation.
Deepseek was better overall regarding artefacts and animation, but fixing the navigation would have taken another prompt. Deepseek v3 0324 won this round, so Deepseek gets one point.
Off to test No 2
Test 2: Leet Code – Problem #2861 Solution
For next test, I will use a hard question for Leet Code: “Power of heroes”. Most of the LLM’s tested earlier solved this problem with good accuracy, let’s see if Deep Seek V3 and Claude Sonnet 3.7 keeps up the pace or not.
Prompt
You are given a 0-indexed integer array nums representing the strength of some heroes. The power of a group of heroes is defined as follows:
Let i0, i1, ... ,ik be the indices of the heroes in a group. Then, the power of this group is max(nums[i0], nums[i1], ... ,nums[ik])2 * min(nums[i0], nums[i1], ... ,nums[ik]). Return the sum of the power of all non-empty groups of heroes possible. Since the sum could be huge, return it modulo 109 + 7.
Example 1:
Input: nums = [2,1,4] Output: 141 Explanation: 1st group: [2] has power = 22 * 2 = 8. 2nd group: [1] has power = 12 * 1 = 1. 3rd group: [4] has power = 42 * 4 = 64. 4th group: [2,1] has power = 22 * 1 = 4. 5th group: [2,4] has power = 42 * 2 = 32. 6th group: [1,4] has power = 42 * 1 = 16. 7th group: [2,1,4] has power = 42 * 1 = 16. All groups' powers are 8 + 1 + 64 + 4 + 32 + 16 + 16 = 141.
Example 2:
Input: nums = [1,1,1] Output: 7 Explanation: A total of 7 groups are possible, and the power of each group will be 1. Therefore, the sum of the powers of all groups is 7.
Constraints:
1 <= nums.length <= 105 1 <= nums[i] <= 109
Optimize the code for time and space complexity and write clearly, concisely and cleanly. Avoid code redundancy
If both models solve the challenge, the evaluation will be based on Time, Space complexity, and response output time.
Let’s check the outputs.
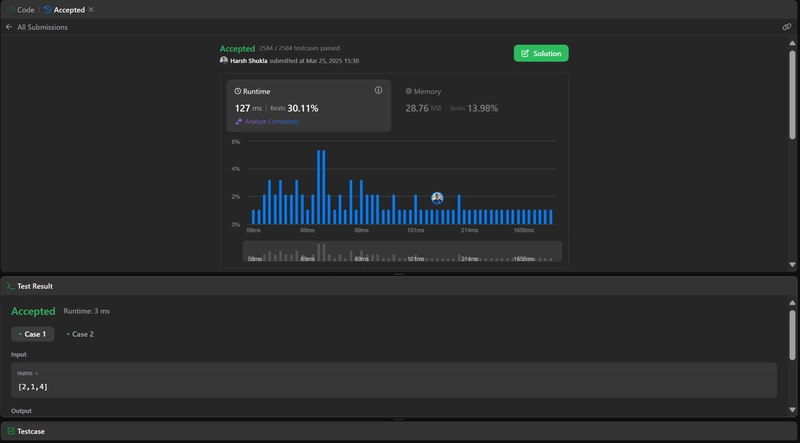
Output: Deep Seek V3 (Code -67.7s )
class Solution:
def sumOfPower(self, nums):
MOD = 10**9 + 7
nums.sort()
n = len(nums)
power_of_two = [1] * n
for i in range(1, n):
power_of_two[i] = (power_of_two[i - 1] * 2) % MOD
res = 0
sum_prev = 0 # This will accumulate the sum of nums[j] * 2^j terms for j < i
for i in range(n):
# The current element can be the max in subsets where it is included, and any subset of previous elements.
# The min in such subsets can be any of the previous elements or itself.
# The contribution when nums[i] is the max: nums[i]^2 * min_of_subset
# The sum over all such subsets is nums[i]^2 * (sum_{S includes nums[i] as max} min(S))
# The sum of min(S) for all S where nums[i] is max and S includes nums[i] and any subset of elements before i:
# For each j <= i, the min is nums[j] and the count is 2^{i-j} if j < i, or 1 if j == i.
# So sum_{j=0 to i} nums[j] * 2^{i-j} when j < i, plus nums[i] * 1 (when j=i)
# This can be rewritten as (sum_{j=0}^{i-1} nums[j] * 2^{i-j}) + nums[i]
# But this is similar to the previous terms multiplied by 2 each step plus nums[i]
# So we can maintain this sum dynamically.
# The term for nums[i] being the max in subsets:
# The sum of min(S) for all subsets S where max(S) = nums[i] is (sum_prev + nums[i])
# Because sum_prev is sum_{j < i} nums[j] * 2^{i-j-1}, but we can compute it incrementally.
current_contribution = (sum_prev + nums[i]) % MOD
term = (nums[i] * nums[i]) % MOD
term = (term * current_contribution) % MOD
res = (res + term) % MOD
# Update sum_prev for next iteration: sum_prev * 2 + nums[i]
sum_prev = (sum_prev * 2 + nums[i]) % MOD
return res
Results
Deep Seek V3 solved the code and handled the Time & Space Complexity as instructed.
As for code quality, it is long, well-explained, documented, straightforward and easy to follow.
Now, let’s see how Sonnet 3.7 Performs!
Output: Claude Sonnet 3.7 Base (Code – 16.5s)
class Solution:
def sumOfPower(self, nums):
MOD = 10**9 + 7
nums.sort()
result = 0
# Process each potential max value
for i in range(len(nums)):
# For single element group
result = (result + nums[i]**3) % MOD
# For groups with more than one element
# Count contribution of this element as max with all possible mins
for j in range(i):
# This is the count of subsets where nums[j] is min and nums[i] is max
# We need to multiply by 2^(i-j-1) to account for all possible subset combinations
# between j and i (excluding j and i)
contribution = (nums[i]**2 * nums[j] * pow(2, i-j-1, MOD)) % MOD
result = (result + contribution) % MOD
return result
Results
Final Thoughts
- Deep Seek V3 code was long, explanatory with high response time, but passed the test cases and handled the time and space complexity
- Sonnet on the other hand responded with shorter cleaner code with low response time but failed to pass the private test cases.
- If I am preparing for Coding Exams & Interviews, I will go for Deep Seek V3 for code references.
Current Score
Score: Deep Seek v3 – 1, Claude Sonnet 3.7 – 0
off to test no 3
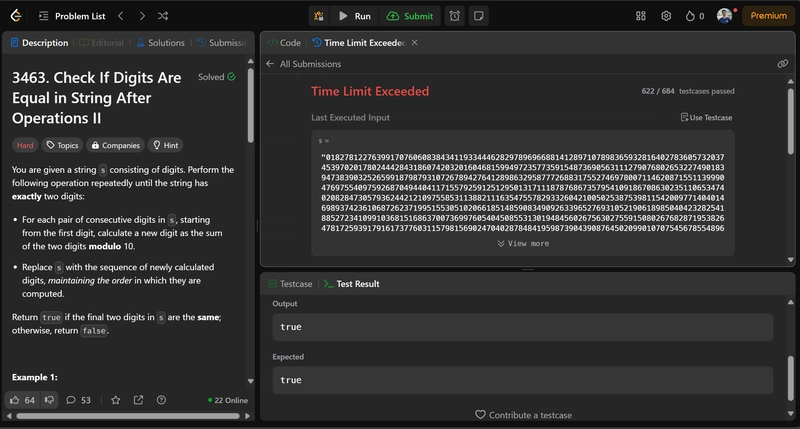
Test 3: Leet Code – Problem #3463 Solution
I found this one while writing my other blog, and it became my benchmark question to evaluate coding capabilities of LLM.
This requires 1st principle thinking, rather than library usage. Let’s see how Deep Seek V3 and Sonnet 3.7 Base performs.
I am personally excited for Deep Seek V3 performance, cause last time only Grok3 (Think Mode) was only able to solve it!
Prompt
I am giving you a leetcode problem with test case, your job is to write a clean and concise code.
The question will have private test cases, so make sure your cover edge cases as well.
You can solve this qn using 1st principle reasoning
Here is the problem Statement :
You are given a string s consisting of digits. Perform the following operation repeatedly until the string has exactly two digits:
For each pair of consecutive digits in s, starting from the first digit, calculate a new digit as the sum of the two digits modulo 10.
Replace s with the sequence of newly calculated digits, maintaining the order in which they are computed.
Return true if the final two digits in s are the same; otherwise, return false.
Example 1:
Input: s = "3902"
Output: true
Explanation:
Initially, s = "3902"
First operation:
(s[0] + s[1]) % 10 = (3 + 9) % 10 = 2
(s[1] + s[2]) % 10 = (9 + 0) % 10 = 9
(s[2] + s[3]) % 10 = (0 + 2) % 10 = 2
s becomes "292"
Second operation:
(s[0] + s[1]) % 10 = (2 + 9) % 10 = 1
(s[1] + s[2]) % 10 = (9 + 2) % 10 = 1
s becomes "11"
Since the digits in "11" are the same, the output is true.
Example 2:
Input: s = "34789"
Output: false
Explanation:
Initially, s = "34789".
After the first operation, s = "7157".
After the second operation, s = "862".
After the third operation, s = "48".
Since '4' != '8', the output is false.
If you look carefully, we have explicitly mentioned that the code needs to be solved using the first principle and must be clear, concise, explanatory, and cover all edge cases.
Though we never mentioned it’s a question about Pascal’s Triangle, figuring it out is part of the model reasoning process.
Let’s see which one can identify and solve it.
Deep Seek V3 Results
Output: Deep Seek V3
def isSameAfterOperations(s: str) -> bool:
while len(s) > 2:
new_s = []
for i in range(len(s) - 1):
new_digit = (int(s[i]) + int(s[i+1])) % 10
new_s.append(str(new_digit))
s = ''.join(new_s)
return s[0] == s[1]
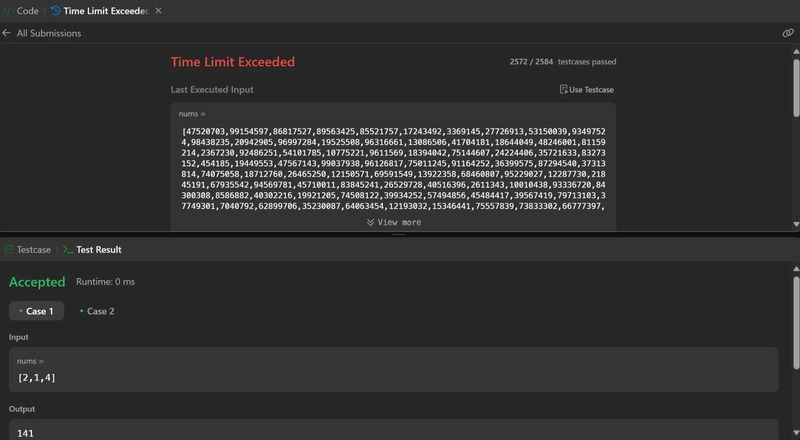
Result
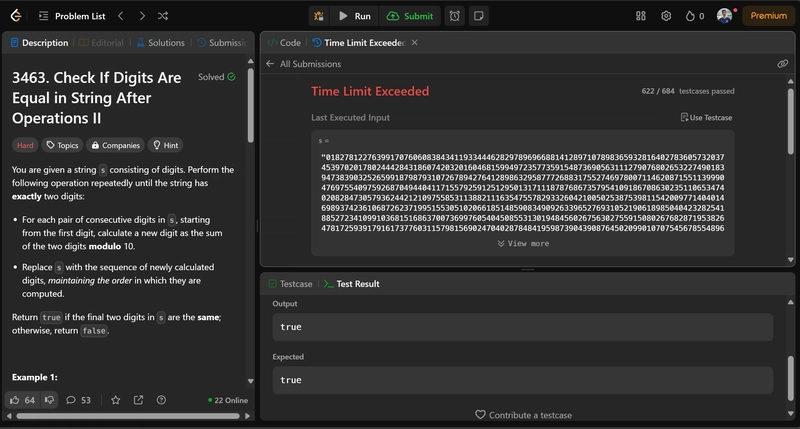
Time Limit Exceeded – Deep Seek V3
Yup, it’s also failed. So Grok3 still keeps its spot!
Though I liked the concise code, I hated the lack of clear comments and the model’s failure to follow the first principal reasoning abilities.
Let’s see how Claude Sonnet 3.7 Performs
Output: Claude Sonnet 3.7
def isSameSequence(s: str) -> bool:
# Continue until we have only two digits
while len(s) > 2:
new_s = ""
# Process each consecutive pair
for i in range(len(s) - 1):
digit1 = int(s[i])
digit2 = int(s[i+1])
new_digit = (digit1 + digit2) % 10
new_s += str(new_digit)
s = new_s
# Check if the two remaining digits are the same
return s[0] == s[1]
As usual, the sonnet verified its steps, which helped it pass the public test cases, but was not enough to pass the private test case, resulting in Time Limit Exceed Error
Time Limit Exceeded – Sonnet 3.7 Base
Though Sonnet also failed, the code was well documented, short and clear. Would go for it!
Final Thoughts
• Deep Seek V3 code was short and concise, but the code was not clear (as there were no comments) & model failed to follow the instructions given in the prompt.
• On the other hand, Sonnet responded with a more extended code, but it was concise and clear and followed the instructions except for the first principal reasoning through the process to follow.
Current Score: Deep Seek v3 -2, Claude Sonnet 3.7 – 0
Off to test No 4
Test 4: Minecraft Game in Python (One Shot Prompting)
Till now we have explored 3D Scene Generation and Coding problem, what about building a complete solution.?
So can’t Deep Seek V3 / Claude Sonnet 3.7 build full stack application, handling all the intricacies, let’s check it out.
For this let’s build a Minecraft game using Python using One-Shot Prompting
Prompt : Build me a very simple Minecraft game using PyGame in Python.
Output: Deep Seek V3
Code: GitHub (deepseek_v3_results.py) + instructions with install instruction.
How to Play:
Left-click to place the selected block
Right-click to remove a block
Click on the inventory at the top to select different block types (grass, dirt, stone)
Features:
Simple world generation with grass, dirt, and stone layers
Basic block placement and removal mechanics
Inventory system to select different block types
Grid-based placement system
Requirements
Python 3.x
Pygame library ( pip install pygame)
Results
As expected, Deepseek V3 wrote the right code on the first try—impressive. It even cloned Minecraft’s building mechanics!
The block palette selection UI isn’t working, and there’s still room for improvement. But overall, I am impressed by the output.
Output: Claude Sonnet 3.7 Base
Code: GitHub (claude_sonnet_3.7_results.py) + instructions with movement details but no install instructions.
How to Play
1. **Movement**:
- A/Left Arrow: Move left
- D/Right Arrow: Move right
- Space: Jump
2. **Interact with Blocks**:
- Left-click: Break a block (adds to inventory)
- Right-click: Place a block (uses from inventory)
3. **Select Blocks**:
- Press 1-6 to select different block types from your inventory
Game Features
- Simple terrain generation with grass, dirt, and stone
- Random tree generation with wood and leaves
- Basic physics with gravity and collision detection
- Simple inventory system
- Camera that follows the player
Results
Never expected this, but program crashed. Based on the output, it is a Type error.
After explicit prompting here is the results(claude_sonnet_3.7_game_results.py):
I expected model to build a Minecraft with functionality to add blocks and movement, but it made something totally different – A 2D Patformer.
No way to delete or add blocks, looks like 2D platformer with wobble effect ((no what was needed)), no button value change in Ui (similar to deep seek v3).
Overall, here are my final thoughts for this test.
Final Thoughts
- Deep Seek V3 was able to mimic some parts of the Minecraft (adding, deleting and selecting blocks), followed physics, wrote good code and ran in 1st try.
- On the other hand, Sonnet 3.7 Base struggled—it needed multiple prompts, failed physics rules, and had a wobbling effect. While it eventually produced working code, it lacked expected functionality (adding, removing and selecting blocks).
- Do note that both models have the potential, and both implement different functionality with same prompt, but Deep Seek V3 code & output was more polished in terms of One Shot Prompting.
- So, 1 point goes to Deep Seek V3
Current Score
Score: Deep Seek v3 -1, Claude Sonnet 3.7 – 0
Who Aces the Test?
After evaluating model responses over multiple test:
- Claude Sonnet 3.7 Base Score: 1/4
- Deep Seek V3 Score: 3/4
Winner: Deep Seek V3
Final Thoughts
As Deep Seek V3 aces the simulation, game building and Leet Code problems (medium difficulty). It scores 3/4 while sonnet was only able to pass 1/4.
So, If I have to pick one, I will definitely go for Deep Seek V3 as it lives up to its Claims (at least in contrast to Sonnet 3.7 Base Model)
However, it is important to note that:
As these models continue to evolve, the gap between them may change, but for now, both represent remarkable capabilities that can help students and developers tackle complex problems across multiple domains.
This content originally appeared on DEV Community and was authored by Developer Harsh