This content originally appeared on HackerNoon and was authored by Phenomenology Technology
:::info Authors:
(1) Dorian W. P. Amaral, Department of Physics and Astronomy, Rice University and These authors contributed approximately equally to this work;
(2) Mudit Jain, Department of Physics and Astronomy, Rice University, Theoretical Particle Physics and Cosmology, King’s College London and These authors contributed approximately equally to this work;
(3) Mustafa A. Amin, Department of Physics and Astronomy, Rice University;
(4) Christopher Tunnell, Department of Physics and Astronomy, Rice University.
:::
Table of Links
2 Calculating the Stochastic Wave Vector Dark Matter Signal
3 Statistical Analysis and 3.1 Signal Likelihood
4 Application to Accelerometer Studies
4.1 Recasting Generalised Limits onto B − L Dark Matter
6 Conclusions, Acknowledgments, and References
\ A Equipartition between Longitudinal and Transverse Modes
B Derivation of Marginal Likelihood with Stochastic Field Amplitude
D The Case of the Gradient of a Scalar
B Derivation of Marginal Likelihood with Stochastic Field Amplitude
The full signal in time space is given by
\

\ Using the series representation of the Bessel function, together with Gamma function identities, the 5 random variables can be integrated out analytically. We arrive at the following marginalized (and normalized) likelihood:
\
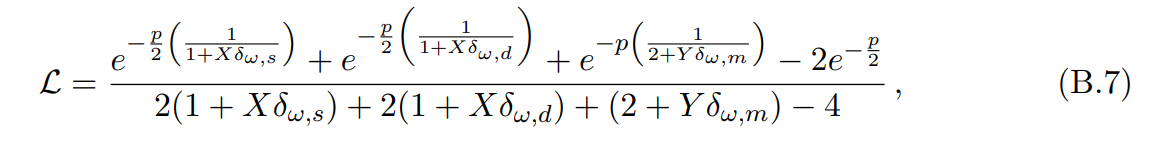
\ where
\
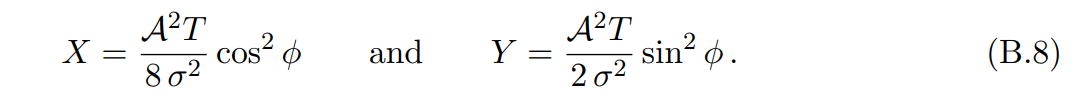
\ This likelihood can be split into three individual likelihoods for the sum/difference peaks and the Compton peak, as given in Eq. (3.2). The form of the likelihoods for the sum and difference peaks is equivalent.
\
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
This content originally appeared on HackerNoon and was authored by Phenomenology Technology